人類的大腦在不斷地進(jìn)化，自然所想的東西也就越來越多，需要探究的問題也就越來越深奧。那么你聽說過無限猴子定理嗎?很多人都不知道無限猴子定理是什么，接下來，小編就來帶你了解什么是無限猴子定理。

什么是無限猴子定理

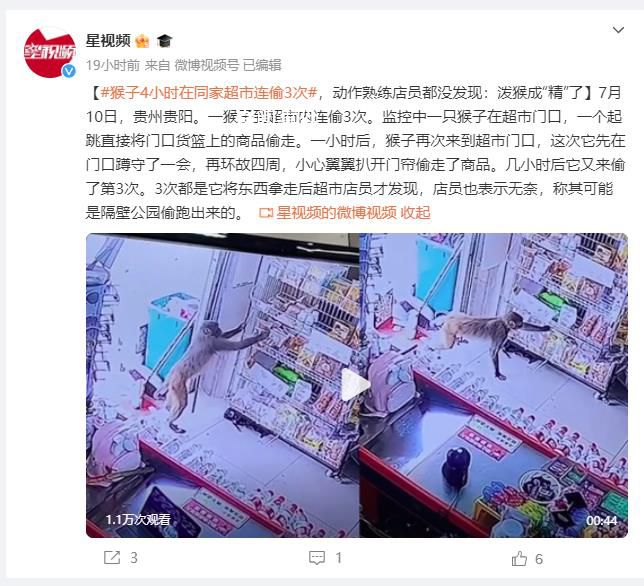
一般關(guān)于此定理的敘述為：有無限只猴子用無限的時(shí)間會產(chǎn)生特定的文章。其實(shí)不必要出現(xiàn)了兩件無限的事物，一只猴子打字無限次已經(jīng)足夠打出任何文章，而無限只猴子則能即時(shí)產(chǎn)生所有可能的文章。

其他取代的敘述，可能是用英國博物館或美國國會圖書館取代法國國家圖書館;另一個(gè)常見的版本是英語使用者常用的，就是猴子會打出莎士比亞的著作。當(dāng)然我們也可以說，這只可憐的猴子能打出整本《西游記》來。

無限猴子定理的出處

無限猴子定理是來自波萊爾一本1909年出版談概率的書籍，當(dāng)中介紹了“打字的猴子”的概念。這個(gè)定理是概率論中的柯爾莫哥洛夫的零一律的其中一個(gè)命題的例子。

零一律是概率論中的一個(gè)定律，它是安德雷·柯爾莫哥洛夫發(fā)現(xiàn)的。其內(nèi)容是：有些事件發(fā)生的概率不是幾乎一(肯定發(fā)生)，就是幾乎零(肯定不發(fā)生)。

這樣的事件被稱為“尾事件”。尾事件是由無限多的隨機(jī)變量的序列來定義的。比如它不是與X1的值無關(guān)。比如假如我們?nèi)訜o限多次銀幣，則連續(xù)100次數(shù)字面向上的事件是一個(gè)尾事件。

無限猴子定理的意義

在現(xiàn)實(shí)中，猴子使用鍵盤時(shí)通常會連按某一個(gè)鍵或拍擊鍵盤，很難產(chǎn)生連貫的語句。雖然真的得到一篇來自于猴子的像樣的文章的幾率幾乎是零，但是這條定理說明了在足夠多次的試驗(yàn)中，概率很低的事件發(fā)生的可能性反而很高。比如雖然買彩票的中獎(jiǎng)概率很低，但是如果一次性買入極大量不同組合的彩票，那么就很可能中彩。

讓我們舉一反三，可以說如果給猴子足夠長的時(shí)間，猴子一定能輸出你的郵箱密碼序列或是生日日期，這個(gè)概率一定大于猴子敲出一篇文章的概率。

無限猴子定理的證明

兩個(gè)獨(dú)立事件同時(shí)發(fā)生概率等于其中每個(gè)事件單獨(dú)發(fā)生概率乘積。比如，在某一天悉尼下雨可能性為0.3，同時(shí)舊金山地震可能性是0.008(這兩個(gè)事件可以視為相互獨(dú)立的)，那么它們同時(shí)發(fā)生概率是 0.3 × 0.008 = 0.0024。

假設(shè)一個(gè)打字機(jī)有50個(gè)鍵，想要打出的字是“banana”。隨機(jī)打字時(shí)，打出第一個(gè)字母“b”的概率是 1/50，打出第二個(gè)字母“a”的概率也是 1/50 ，因?yàn)槭录?dú)立，所以一開始就打出單詞“banana”概率是：

(1/50) × (1/50) ×(1/50) × (1/50) × (1/50) × (1/50) = (1/50)6, 這個(gè)概率小于150億分之1。 同理，接下來繼續(xù)打出“banana”的概率也是(1/50)6。

所以，在給定6個(gè)字母中沒打出“banana”概率是1 − (1/50)6。因?yàn)槊恳欢?6個(gè)字母)文字都是獨(dú)立的，連續(xù)n段都沒有打出“banana”概率Xn是：

隨著n變大，Xn在變小。當(dāng)n等于100萬時(shí)，Xn大約是0.9999(沒有打出“banana”的概率是99.99%);但是當(dāng)n等于100億時(shí)Xn大約是0.53(沒有打出“banana”的概率是53%);當(dāng)n等于1000億時(shí)Xn大約是0.0017(沒有打出“banana”概率是0.17%);當(dāng)n趨于無窮時(shí)Xn趨于零。這就是說，只要使n足夠大，Xn可以變得足夠小。

同樣論證也可說明在無限多猴子中有至少一個(gè)會打出一段特定文章。這里Xn = (1 −(1/50)6)n，其中，Xn表示在前n個(gè)猴子中沒有一個(gè)一次打出banana的概率。當(dāng)我們有1000億只猴子時(shí)，這個(gè)概率降到0.17%，并且隨著猴子數(shù)量n趨于無窮大，沒打出“banana”概率Xn趨于0。原文地址：http://www.yi2.net/article/201606/13155.html

但是，只有有限時(shí)間和有限只猴子時(shí)，結(jié)論就大不一樣了。如果猴子數(shù)量和可觀測宇宙中基本粒子數(shù)量一樣多，大約1080只，每秒打1000個(gè)字，持續(xù)打100倍于宇宙生命長度時(shí)間(大約1020秒)有猴子能夠打出一本很薄書的概率也接近與0。

無限猴子定理的應(yīng)用

無限猴子定理本身概念并不復(fù)雜，但實(shí)際上卻是難以應(yīng)用。因?yàn)槲覀冋也坏阶銐蚯液戏ǖ暮镒?動保人士必然會抗議)，我們也沒有耐心等足夠久讓他們寫出一本曠世名作。然而，就在最近卻有個(gè)年輕人意外地利用網(wǎng)絡(luò)，進(jìn)行了一項(xiàng)大規(guī)模的猴子實(shí)驗(yàn)——他把全世界數(shù)以萬計(jì)坐在電腦前的人都當(dāng)成了猴子。

一星期前，一個(gè)名為 twitchplayspokemon 的帳號在知名線上直播網(wǎng)站 twitch 開啟了「神奇寶貝紅版」的直播。這款 1996 年在日本發(fā)行的掌上游戲在當(dāng)時(shí)引領(lǐng)起一股神奇寶貝旋風(fēng)，其后續(xù)系列作至今也在全世界累積了數(shù)以億計(jì)的游戲人口。

神奇寶貝紅版是一款開放式無限時(shí)可存檔的單人游戲，玩家們可以按照攻略滿足條件一路闖關(guān)，也可以自己的步調(diào)體驗(yàn)游戲劇情。然而，和以往觀眾們線上即時(shí)收看實(shí)況主在游戲中一舉一動，同時(shí)在聊天室評論的形式不同。這一次是由所有的觀眾來決定游戲里的角色該怎么行動。觀眾們只要在聊天室里打出上(up) 下(down) 左(left) 右(right) 確定(A) 取消(B)，就能讓游戲里的主角 Red 依照對應(yīng)的指令行動。

這個(gè)頻道推出不滿一周，累計(jì)已吸引了兩千萬人次點(diǎn)閱，同時(shí)上線觀看的人數(shù)也高達(dá)十萬人。人人都想輸入指令去操縱主角 Red 的動作。甚至因?yàn)橥瑫r(shí)下指令的人太多，造成指令往往會延遲個(gè)近一分鐘。這樣也間接造成了所有操控者輸入的指令經(jīng)常互相抵銷彼此矛盾。甚至往往 Red 想直走前進(jìn)個(gè)幾步，都需要個(gè)幾十分鐘。不論是理性想破關(guān)的玩家還是隨性惡搞的玩家，他們的指令淨(jìng)效果都可以被看作是近似隨機(jī)分布的。

然而，看似無法在短期內(nèi)破關(guān)的游戲，卻在游戲開始的數(shù)小時(shí)后有了進(jìn)展。玩家們奇跡似的突破了一關(guān)又一關(guān)(失敗了幾千次)，闖過了一個(gè)又一個(gè)迷宮。在實(shí)況主進(jìn)一步引進(jìn)民主(Democracy)—— 20 秒接收一次由期間內(nèi)投票統(tǒng)計(jì)多數(shù)決結(jié)果的指令取代暴民(Anarchy)——原本的模式之后。至今已經(jīng)闖過四分之三的游戲進(jìn)度，破關(guān)在即。

這實(shí)驗(yàn)同時(shí)也是語言資訊學(xué)上的一種具體展現(xiàn)。若我們把所有的指令都連在一起當(dāng)成一組長字串，并且嘗試著加上一些簡單條件讓猴子們能更快打出可以破關(guān)的字串。那我們有以下的方法可以讓這隨機(jī)過程更接近「合理」要求。

我們可以嘗試以下的方法來產(chǎn)生隨機(jī)指令(字串)：

每項(xiàng)指令都有同等的機(jī)率

依照常見與否，賦予各項(xiàng)指令不同的機(jī)率

每項(xiàng)指令的機(jī)率隨前一項(xiàng)指令而變

若以英文的 26 個(gè)字母和空格為例：

所有字母機(jī)率皆相等(1/27) → “RX KHRJFFJUJ”

常見的字母(母音)有更高的機(jī)率 → “OCRO HLI”

相鄰字母彼此不為獨(dú)立事件 → “TEASONARE”

可以看出從 1. 到 3.，字串符合所謂拼音規(guī)則的傾向越來越明顯。這些隨機(jī)過程的產(chǎn)物在加上些許的條件限制以后不再像是隨機(jī)亂碼，反而看起來就像是一些不常見的冷僻單字。就算是目不識丁的猴子，在給定某些條件的限制之下，似乎也有著成為明日文壇新秀的資質(zhì)。

若是對照起這實(shí)驗(yàn)的話，則如下：

觀眾隨機(jī)敲打游戲指令

觀眾(理性)看著游戲畫面并據(jù)此行動使得不合理指令機(jī)率相對下降

民主(Democracy)：在預(yù)期理性玩家多于隨性玩家的前提下進(jìn)行

如此一來，在加上簡單條件以后，字串(指令)的有效(合理)性便顯著提升。

這也說明了，為何乍看之下永遠(yuǎn)玩不完的神奇寶貝紅版，能在短短一周內(nèi)幾乎破關(guān)。只要給予限制的條件合理，隨機(jī)過程演算也可以在一定時(shí)間內(nèi)收斂到「合理」的結(jié)果。而這樣的概念也被引入許多複雜演算領(lǐng)域中。

無限猴子定理在現(xiàn)實(shí)生活中的應(yīng)用

在現(xiàn)實(shí)中，猴子使用鍵盤時(shí)通常會連按某一個(gè)鍵或拍擊鍵盤，很難產(chǎn)生連貫的語句。雖然真的得到一篇來自于猴子的像樣的文章的幾率幾乎是零，但是這條定理說明了在足夠多次的試驗(yàn)中，概率很低的事件發(fā)生的可能性反而很高。比如雖然買彩票的中獎(jiǎng)概率很低，但是如果一次性買入極大量不同組合的彩票，那么就很可能中彩。

讓我們舉一反三，可以說如果給猴子足夠長的時(shí)間，猴子一定能輸出你的郵箱密碼序列或是生日日期，這個(gè)概率一定大于猴子敲出一篇文章的概率。